-
Notifications
You must be signed in to change notification settings - Fork 111
“等一下,我碰!”——常见的2D碰撞检测 #8
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Comments
|
讲的很清楚而且还有代码实例,非常好的文章! |
|
非常感谢,刚好在学习这个。。。给个赞,感谢用心的付出 |
|
好文~ |
wuyxp
pushed a commit
to wuyxp/html-test
that referenced
this issue
Apr 20, 2018
|
圆形与矩形碰撞
应该是大于号吧 |
|
@yansixing 非常感谢指出错误,已修正😆 |
|
用 issue 来写 blog 这种形式也是棒棒的,哈哈哈,讲的很清楚,多谢啦 |
当时不想维护 hexo 静态博客就迁移到 github 的 issues 了。但这也有缺点,比如说:
|
|
@ @ 赞不绝口 |
|
用issue来写博客的创意很好啊,学到了 |
但是用github写文自带流量,哈哈哈 |
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment
“碰乜鬼嘢啊,碰走晒我滴靓牌”。想到“碰”笔者就自然联想到“麻将”这一伟大发明。当然除了“碰”,洗牌的时候也充满了大量『碰撞』。
好了,不废话。直入主题——碰撞检测。
在 2D 环境下,常见的碰撞检测方法有如下几种:
下文将以由易到难的顺序介绍上述各种碰撞检测方法:外接图形判别法 > 其他 > 光线投射法 > 分离轴定理。
另外,有一些场景只需约定好限定条件,也能实现我们想要的碰撞,如下面的碰壁反弹:
See the Pen Boundary collision detection by Jc (@JChehe) on CodePen.
<script async src="https://production-assets.codepen.io/assets/embed/ei.js"></script>当球碰到边框就反弹(如
x/y轴方向速度取反)。再例如当一个人走到
100px位置时不进行跳跃,就会碰到石头等等。因此,某些场景只需通过设定适当的限制即可实现碰撞检测。
外接图形判别法
轴对称包围盒(Axis-Aligned Bounding Box)
概念:判断任意两个(无旋转)矩形在每个轴上是否重叠,若都重叠则为碰撞。
算法:
两矩形间碰撞的各种情况:
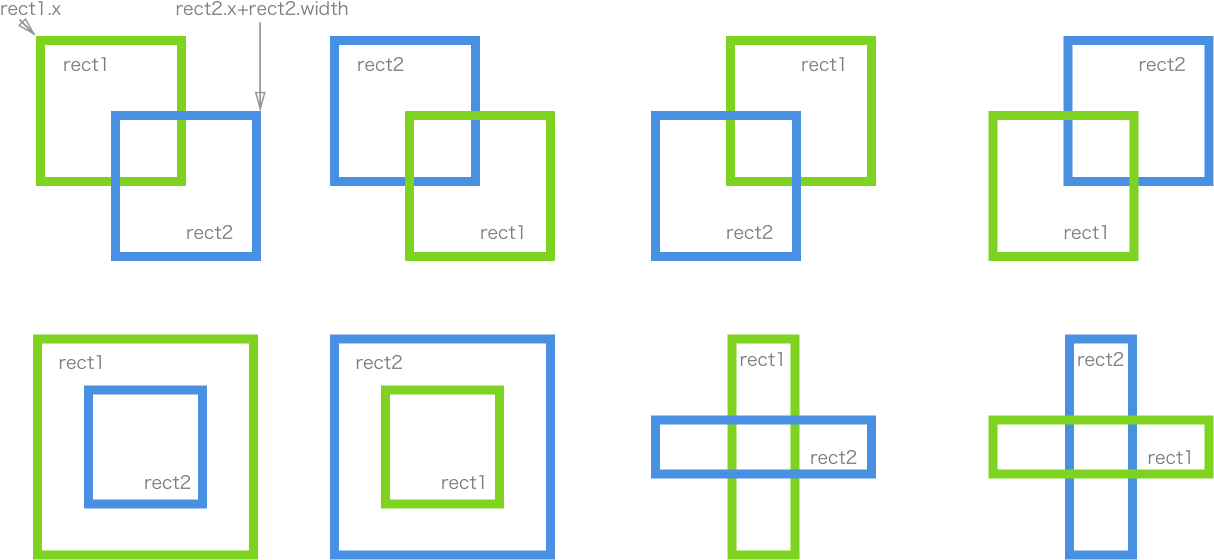
在线运行示例(先点击运行示例以获取焦点,下同):
See the Pen AxisAlignedBoundingBox collision detection by Jc (@JChehe) on CodePen.
<script async src="https://production-assets.codepen.io/assets/embed/ei.js"></script>圆形碰撞(Circle Collision)
概念:通过判断任意两个圆形的圆心距离是否小于两圆半径之和,若小于则为碰撞。
计算两点距离的公式:
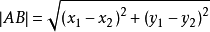
判断两圆心距离是否小于两半径之和:
图例:
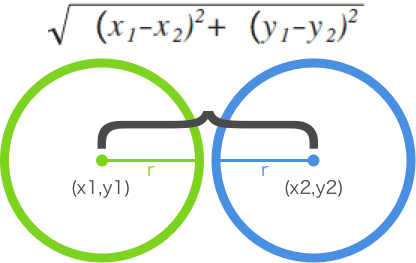
在线运行示例:
See the Pen EZrorG by Jc (@JChehe) on CodePen.
<script async src="https://production-assets.codepen.io/assets/embed/ei.js"></script>圆形与矩形(无旋转)
概念:通过找出矩形上离圆心最近的点,然后通过判断该点与圆心的距离是否小于圆的半径,若小于则为碰撞。
那如何找出矩形上离圆心最近的点呢?下面我们从 x 轴、y 轴两个方向分别进行寻找。为了方便描述,我们先约定以下变量:
首先是 x 轴:
如果圆心在矩形的左侧(
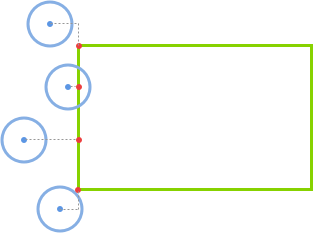
if(circle.x < rect.x)),那么closestPoint.x = rect.x。如果圆心在矩形的右侧(
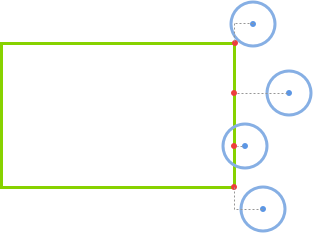
else if(circle.x > rect.x + rect.w)),那么closestPoint.x = rect.x + rect.w。如果圆心在矩形的正上下方(
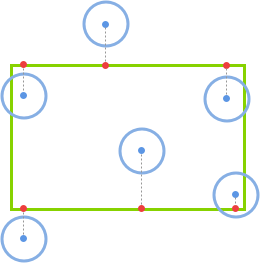
else),那么closestPoint.x = circle.x。同理,对于 y 轴(此处不列举图例):
如果圆心在矩形的上方(
if(circle.y < rect.y)),那么closestPoint.y = rect.y。如果圆心在矩形的下方(
else if(circle.y > rect.y + rect.h)),那么closestPoint.y = rect.y + rect.h。圆心在矩形的正左右两侧(
else),那么closestPoint.y = circle.y。因此,通过上述方法即可找出矩形上离圆心最近的点了,然后通过『两点距离公式』得出『最近点』与『圆心』的距离,最后将其与圆的半径相比,即可判断两者是否发生碰撞。
在线运行示例:
See the Pen Circle and Rectangle by Jc (@JChehe) on CodePen.
<script async src="https://production-assets.codepen.io/assets/embed/ei.js"></script>圆形与旋转矩形(以矩形中心为旋转轴)
概念:即使矩形以其中心为旋转轴进行了旋转,但是判断它与圆形是否发生碰撞的本质还是找出矩形上离圆心的最近点。
对于旋转后的矩形,要找出其离圆心最近的点,似乎有些困难。其实,我们可以将矩形的旋转看作是整个画布的旋转。那么我们将画布(即 Canvas)反向旋转『矩形旋转的角度』后,所看到的结果就是上一个方法“圆形与矩形(无旋转)”的情形。因此,我们只需计算画布旋转后的圆心位置,即可使用『圆形与矩形(无旋转)』的判断方法了。
先给出可直接套用的公式,计算反向旋转后的圆心坐标:
下面给出该公式的推导过程:
根据下图,计算某个点绕另外一个点旋转一定角度后的坐标。我们设 A(x,y) 绕 B(a,b) 旋转 β 度后的位置为 C(c,d)。
由上述公式推导后可得:旋转后的坐标 (c,d) 只与旋转前的坐标 (x,y) 及旋转的角度 β 有关。
当然,(c,d) 是旋转一定角度后『相对于旋转点(轴)的坐标』。因此,前面提到的『可直接套用的公式』中加上了矩形中心点的坐标值。
从图中也可以得出以下结论:由 A 点旋转后得到的 C 点总是在圆周(半径为 |AB|)上运动,利用这点可让物体绕旋转点(轴)做圆周运动。
得到旋转后的圆心坐标值后,即可使用『圆形与矩形(无旋转)』方法进行碰撞检测了。
在线运行案例:
See the Pen Circle and Rotated Rectangle Collision Detection by Jc (@JChehe) on CodePen.
<script async src="https://production-assets.codepen.io/assets/embed/ei.js"></script>其他
地图格子划分
概念:将地图(场景)划分为一个个格子。地图中参与检测的对象都存储着自身所在格子的坐标,那么可认为当两个物体在相邻格子时即为碰撞,或者两个物体在同一格时才为碰撞。另外,采用此方法的前提是:地图中所有参与碰撞的物体大小都须为格子的整数倍。
蓝色X为障碍物:实现方法:
在线运行示例:
See the Pen map cell collision detection by Jc (@JChehe) on CodePen.
<script async src="https://production-assets.codepen.io/assets/embed/ei.js"></script>适用案例:
像素检测
概念:以像素级别检测物体之间是否存在像素重叠,若存在则为碰撞。
实现方法有多种,下面列举在 Canvas 中的两种实现方式:
globalCompositeOperation = 'destination-in'属性。该属性会使得两者重叠部分保留,其余区域变成透明。因此,若存在非透明像素,则为碰撞。注意,当待检测碰撞物体为两个时,第一种方法需要两个 offscreen canvas,而第二种只需一个。
当然,我们这里并不是利用
offscreen render的性能优势,而是利用offscreen canvas保存独立物体的像素。换句话说:onscreen canvas 只是起展示作用,碰撞检测是在 offscreen canvas 中进行。另外,由于需要逐像素判断,若对整个 Canvas 内所有像素都进行此操作,无疑会浪费很多资源。因此,我们可以先通过运算得到两者相交区域,然后只对该区域内的像素进行检测即可。
图例:
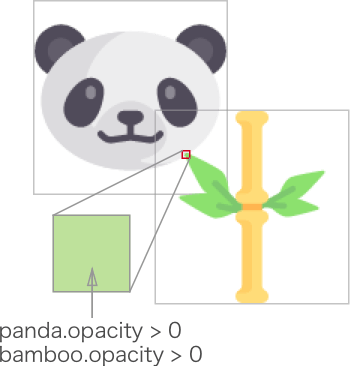
下面示例展示了第一种实现方式:
See the Pen pixel collision detection by Jc (@JChehe) on CodePen.
<script async src="https://production-assets.codepen.io/assets/embed/ei.js"></script>缺点:
光线投射法(Ray Casting)
概念:通过检测两个物体的速度矢量是否存在交点,且该交点满足一定条件。
对于下述抛小球入桶的案例:画一条与物体速度向量相重合的线(
#1),然后再以另一个待检测物体为始点,连线到前一个物体,绘制第二条线(#2),最后根据两条线的交点位置来判定是否发生碰撞。抛球进桶图例:
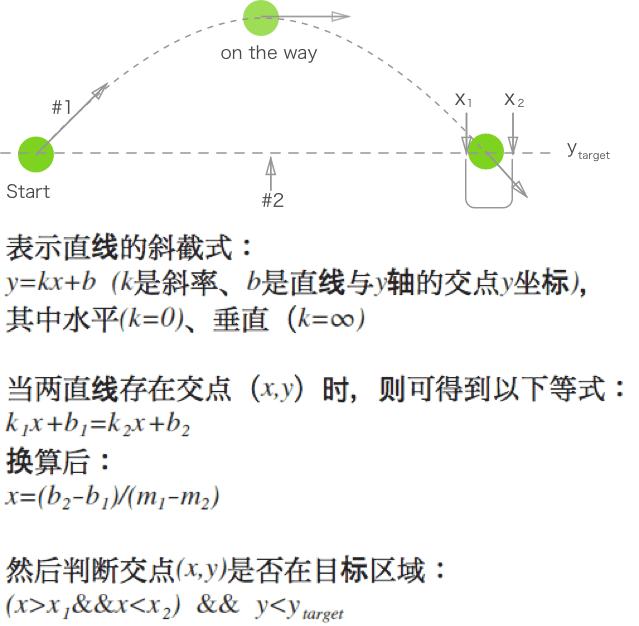
在小球飞行的过程中,需要不断计算两直线的交点。
当满足以下两个条件时,那么就可以判定小球已落入桶中:
#2)下方在线运行示例:
See the Pen ray casting collision detection by Jc (@JChehe) on CodePen.
<script async src="https://production-assets.codepen.io/assets/embed/ei.js"></script>分离轴定理(Separating Axis Theorem)
概念:通过判断任意两个
凸多边形在任意角度下的投影是否均存在重叠,来判断是否发生碰撞。若在某一角度光源下,两物体的投影存在间隙,则为不碰撞。图例:
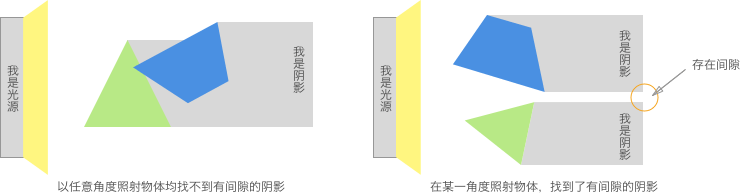
在程序中,遍历所有角度是不现实的。那如何确定
投影轴呢?其实投影轴的数量与多边形的边数相等即可。注:数字标号的含义,在下面“投影轴”章节了解。
以较高抽象层次判断两个凸多边形是否碰撞:
上述代码有几个需要解决的地方:
投影轴
如下图所示,我们使用一条从 p1 指向 p2 的向量来表示多边形的某条边,我们称之为边缘向量。在分离轴定理中,还需要确定一条垂直于边缘向量的法向量,我们称之为“边缘法向量”。
投影轴平行于边缘法向量。投影轴的位置不限,因为其长度是无限的。该轴的方向才是关键的。
以下是向量对象的部分实现,具体可看源码。
向量相减
关于向量的更多知识可通过其它渠道学习。
投影
投影的大小:通过将一个多边形上的每个顶点与原点(0,0)组成的向量,投影在某一投影轴上,然后保留该多边形在该投影轴上所有投影中的最大值和最小值,即可表示一个多边形在某投影轴上的投影了。
判断两多边形的投影是否重合:
projection1.max > projection2.min && project2.max > projection.min为了易于理解,示例图将坐标轴
原点(0,0)放置于三角形边1投影轴的适当位置。由上述可得投影对象:
如何得到向量在投影轴上的长度?
向量点积的几何含义之一是:一个向量在另一个向量方向上的投影长度。
故投影的长度为
x1 * x2 + y1 * y2。圆形与多边形之间的碰撞检测
尽管圆形可看成一个有无数条边组成的正多边形,但我们不可能按照这些边一一进行投影和判断。我们只需将圆形投影到一条投影轴上即可,这条轴就是圆心与多边形顶点中最近一点的连线,如图所示:
因此,该投影轴和多边形自身的投影轴就组成了一组待检测的投影轴数组了。
而对于圆形与圆形之间的碰撞检测依然是两圆心距离是否小于两半径之和。
分离轴定理的整体代码实现,可查看以下案例:
See the Pen SeparatingAxisTheorem by Jc (@JChehe) on CodePen.
<script async src="https://production-assets.codepen.io/assets/embed/ei.js"></script>缺点:
关于分离轴定理的更多资料:
延伸:最小平移向量(MIT)
通常来说,如果碰撞之后,碰撞双方依然存在,那么就需要将两者分开。可以使原来相撞的两物体彼此弹开,也可以让他们黏在一起,还可以根据具体需要来实现其他行为。不过首先要做的还是将两者分开,这就需要用到最小平移向量(Minimum Translation Vector, MIT)。
碰撞性能优化
若每个周期都对全部物体进行两两判断,会造成浪费(因为物体分布在不同区域,不同区域的物体根本不会发生碰撞)。所以,更优的方案是将碰撞分为两个阶段:粗略和精细(broad/narrow)。
粗略阶段(Broad Phase)
粗略阶段能为你提供有可能碰撞的实体列表。这可通过一些特殊的数据结构实现,它们能为你提供这些信息:实体存在哪里和哪些实体在其周围。这些数据结构可以是:四叉树(Quad Trees)、R树(R-Trees)或空间哈希映射(Spatial Hashmap)等。
读者若感兴趣,可以自行查阅相关资料。
精细阶段(Narrow Phase)
当有了较小范围的实体列表,再通过精细阶段的算法(即上述碰撞算法)得到一个确切的答案(是否发生碰撞)。
最后
碰撞检测有多种,选择合适最重要。
完!
参考资料
The text was updated successfully, but these errors were encountered: